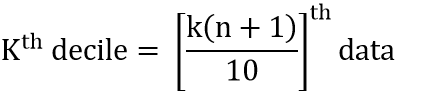Blog Worksheets Examples Practice Problems FAQs

Decile Calculator

How to Use Decile Calculator?

Calculating deciles manually may be time-consuming and carries the risk of errors. However, our decile calculator saves your precious time and gives accurate results. Just follow these steps to use this Calculator:

Enter the values in the input box ensuring commas separate them.
Click on a blue calculate button.
The solution will appear along with step-by-step calculations in a few seconds.
Click on the Reset button to calculate the new problem.

This Decile Calculator is a useful tool for calculating the deciles (1^st to 10^th) of any ungrouped (or raw) data. Our calculator provides an easy and efficient way to calculate deciles while reducing the possibility of errors.

Moreover, this calculator also calculates essential statistical measures such as the Minimum value, Maximum value, Mean, Range, and Sum of the data set.

What is Decile in the Statistics?

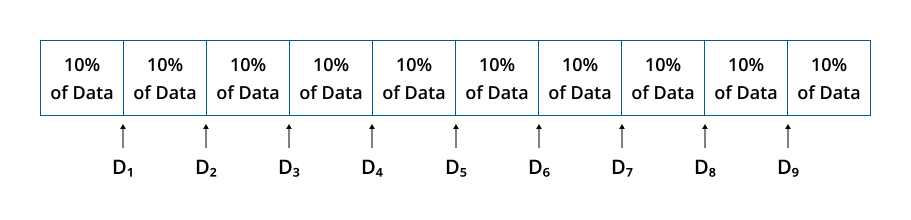
In statistics, a decile is any nine values that divide a sorted dataset into 10 equal parts with each part representing 10% of the data’s distribution.

decile range

Decile Formula for Raw Data

The formula to calculate the k^th decile for raw data is:

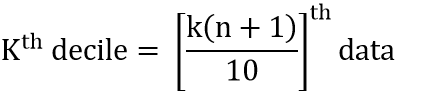
decile formula

Where,

n is the total number of observations in the dataset
k ranges from 1 to 9 for each respective decile.

How to Calculate Decile?

Let us consider some examples to learn how to find a decile.

Example 1:

Find the 3^rd Deciles of the following dataset:

48, 9, 18, 21, 15, 12, 17, 81, 78, 5

Solution:

Step 1: Arrange the data from the smallest to largest values.

5, 9, 12, 15, 17, 18, 21, 48, 78, 81

Step 2: Count the total number of observations in the dataset and denote it as n.

n = 10

Step 3: Use the Decile formula to calculate D₃.

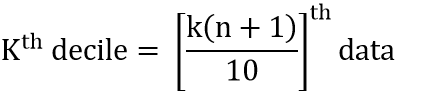
decile formula

For 3^rd Decile:

K = 3

n = 10

∴ K^th decile = [{k (n + 1)} / 10]^th data

3^rd decile = [{3 (10 + 1)} / 10]^th data

= [{3 (11)} / 10]^th data

= [33 / 10]^thdata

3^rd decile = [3.3]^th data

Step 4: Separate the Integer and Fractional Parts of the obtained values of step 3.

3^rd decile = 3^th + 0.3^th data

Step 5: For “(0.3)^th data” subtract 3^rd term from the 4^th term, and then multiply it by “(0.3)”

3^rd decile = 3^th + [0.3 × (4^th – 3^th)]

Step 6: Substitute the values of terms from the sorted data set.

3^rd decile = 12 + [0.3 × (15 − 12)]

= 12 + [0.3 × (3)]

= 12 + (0.9)

3^rd decile = 12.9

Thus, 3^rd decile is 12.9

Example 2:

Calculate D₈of the data set: 68, 51, 28, 5, 41, 29, 19, 4, 14, 34

Solution:

Step 1: Sort the given data set in ascending order.

4, 5, 14, 19, 28, 29, 34, 41, 51, 68

Step 2: Identify Total Observations (n).

n = 10

Step 3: Use the Decile formula to calculate D₈.

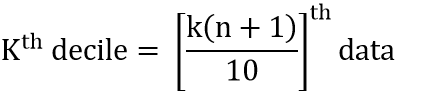
decile formula

For 8^th Decile:

K = 8

n = 10

∴ K^th decile = [{k (n + 1)} / 10]^th data

8^th decile = [{8 (10 + 1)} / 10]^th data

= [{8 (11)} / 10]^th data

= [88 / 10]^thdata

= [8.8]^th data

8^th decile = 8^th + 0.8^th data

Step 4: For “(0.8)^th data” subtract 8^th term from the 9^th term, and then multiply it by “(0.8)”

8^th decile = 8^th + [0.8 × (9^th – 8^th)]

Step 4: Substitute the values of terms from the sorted data set.

8^th decile = 41 + [0.8 × (51 − 41)]

= 41 + [0.3 × (10)]

= 41 + (8)

8^th decile = 49

Therefore, the 8^th decile is 49

Decile Calculator

How to Use Decile Calculator?

What is Decile in the Statistics?

Decile Formula for Raw Data

How to Calculate Decile?

Recent Blogs

Related Tools