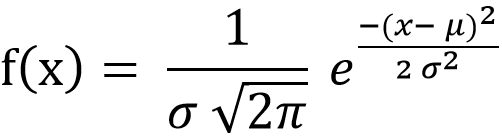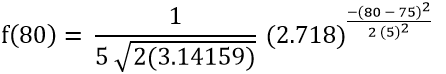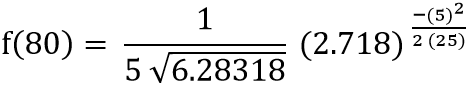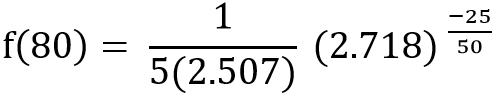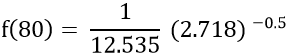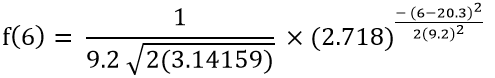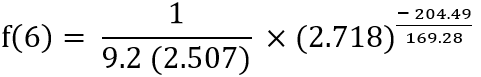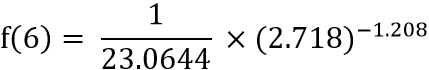This free online calculator calculates the probability density function for normal distribution using the means, standard deviation, and the specific point where function x is to be evaluated.
What is the Probability Density Function (PDF)?
In statistics, a probability function that describes the density of any continuous random variable within a specific range of values is called a probability density function or probability distribution function.
The PDF must always be non-negative and the integral of the probability distribution function over the entire range of possible values for the random variable should be equal to one.
Note
The PDF itself does not give the probability of a specific value but rather the probability density at that point.
Formula to Calculate Probability Density Function for Normal Distribution
The probability density function (PDF) for a normal distribution (also known as a Gaussian distribution) can be calculated by the following formula:
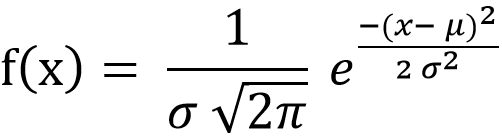
- f(x) is the probability density function.
- x denotes the quantity for which probability is to be calculated.
- σ is the standard deviation.
- π (pi) is a mathematical constant (π ≅ 3.14159)
- e is a Euler constant (e ≅ 2.718)
- μ is the mean of the distribution.
How to Find PDF for Data Set (or Ungrouped Data)?
Let’s learn how to find the probability density function if the means and standard deviation are not given directly.
- First, find the mean by adding up all the values in the dataset and dividing it by the number of data sets.
i.e. means = (x1, x2, x3, …, xn) / n
- Use the above formula to find the standard deviation σ.
σ = √ ((Σ(xi - x̄)2) / n)
- Consider the number of data sets as n.
- Now, put the values of mean, standard deviation, and x into the formula of the probability density function and simplify it.
Examples of Probability Density Function (PDF)
Use the above Probability Density Function Calculator to calculate (PDF) to save time and get error-free results. Alternatively, you can manually compute the PDF using the examples given below.
Example 1: (When Raw Score, Means, and Standard deviation are given)
Find the Probability Density Function (PDF) for a raw score of 80 with a mean of 75 and a standard deviation of 5.
Solution:
Step 1: Identify the parameters required for the formula.
In this example,
Raw score (x) = 80
Means (μ) = 75
Standard deviation (σ) = 5
Also, we know that
π ≅ 3.14159
e ≅ 2.718
Step 2: Substitute the values of x, μ, σ, π, and e into the PDF formula.
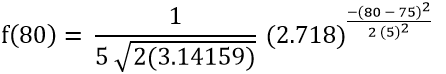
Step 3: Simplify the obtained result from step 2.
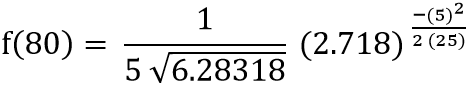
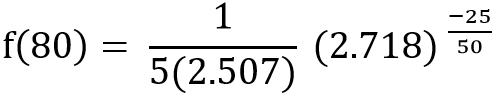
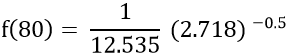
f(80) = 0.08 × 0.607
f(80) = 0.04856
Example 2: (For Dataset or Ungrouped Data)
Find the Probability Density Function (PDF) of Normal distribution for the following data set:
15, 27, 9, 26, 34, 11
Solution:
Step 1: Calculate the Mean (μ) and Standard Deviation (σ) for the given Dataset.
Means (μ) = (15 + 27 + 9 + 26 + 34 + 11) / 6
Means (μ) = 20.3
To calculate Standard deviation.
| Data Set (xi) | xi - x̄ | (xi - x̄)2 |
| 15 | 15 - 20.3 = 5.3 | 28.09 |
| 27 | 27 - 20.3 = 6.7 | 44.89 |
| 9 | 9 - 20.3 = - 11.3 | 127.69 |
| 26 | 26 - 20.3 = 5.7 | 32.49 |
| 34 | 34 - 20.3 = 13.7 | 187.69 |
| 11 | 11- 20.3 = - 9.3 | 86.49 |
| ----- | ----- | Σ(xi - x̄)2 = 507.34 |
∴ σ = √ ((Σ(xi - x̄)2) / n)
σ = √ (507.34 / 6)
σ = √ (84.72578)
Standard deviation = σ = 9.2
Step 2: Put the following values into the PDF formula.
Raw score (x) = Total number of data sets = 6
Means (μ) = 20.3
Standard deviation = σ = 9.2
π ≅ 3.14159
e ≅ 2.718
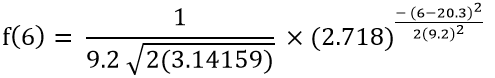
Step 3: Simplify the obtained result from step 2.
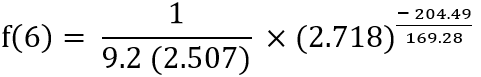
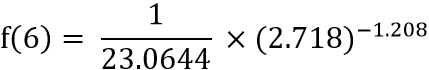
f(6) = 0.043 × 0.299
f(6) = 0.01286
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
