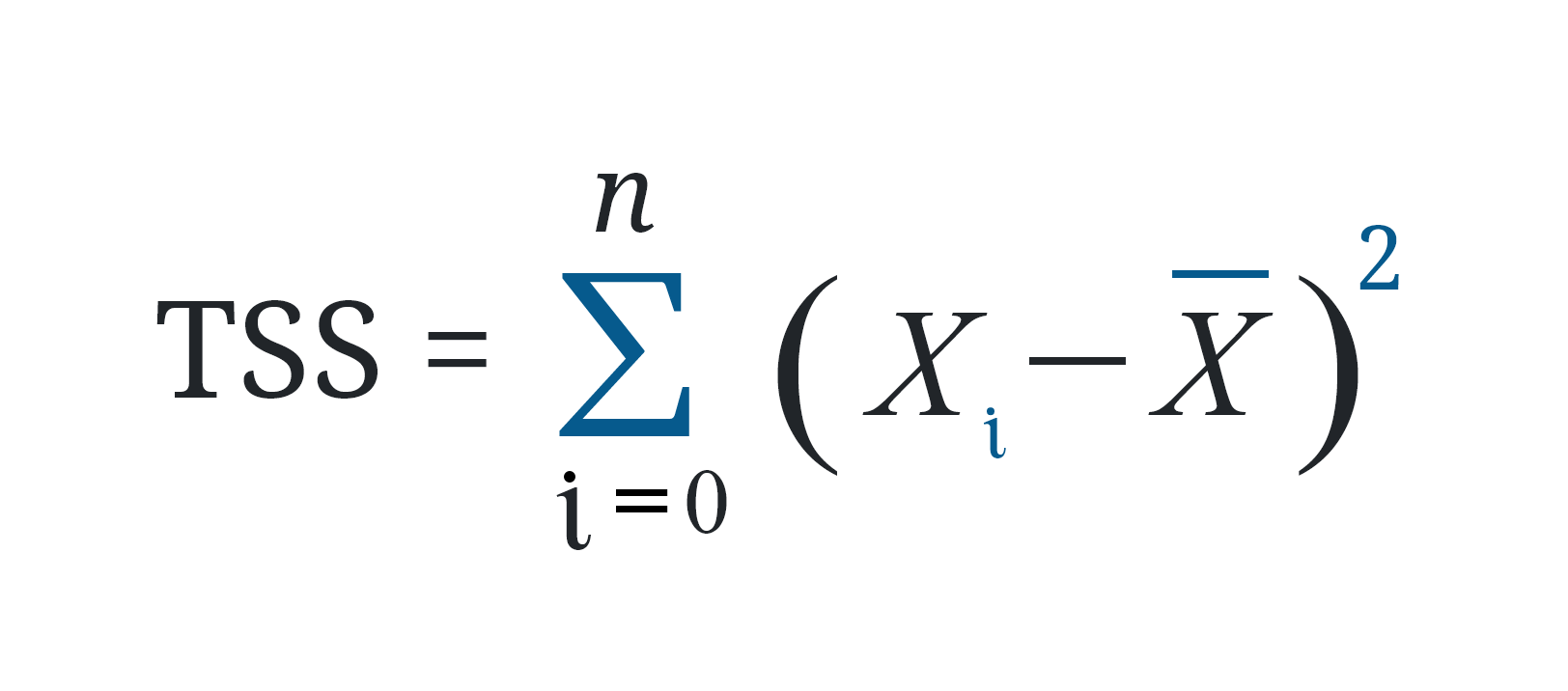Sum of Squares Calculator

The sum of squares calculator is a tool used to simplify and get the sum of squares for a particular collection of data.

What is the sum of squares?

A statistical method for calculating variance in a set of data points is the sum of squares. In particular, it calculates the total squared deviations from the data set's mean. In other words, it reveals how dispersed the data are concerning example the average value.

Formula:

The formula for the sum of squares in statistics is as follows:

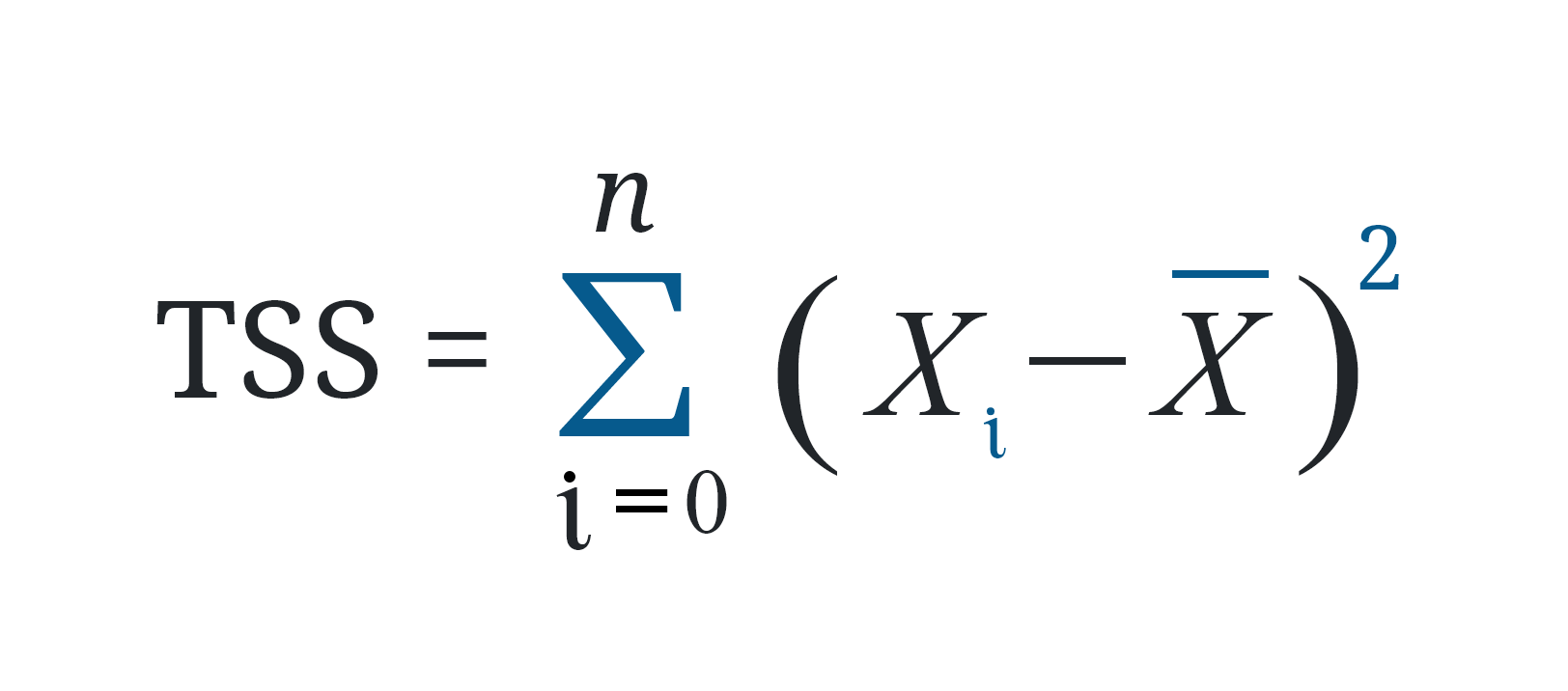
• TSS = The sum of squares
• ∑ = sum of all squares
• i = initial point
• n = total number
• X_i = specific data point
• x̄ = mean of the data set

Note:

(Mean = total sum / total numbers)

The algebraic sum of squares is calculated as follows:

The Sum of the squares = (1)² + (2)² + (3)² + ... + (n)²

How to determine the sum of the squares manually?

You must do the following actions to determine the sum of squares for a collection of data:

1. Determine the data set's average.
2. Determine each data point's deviation from the mean square for each of these variations.
3. Total the squared discrepancies.

Example section:

In this section, we will solve the examples of the sum of the squares step by step,

Example 1:

Find the squared sum of the following data:

9, 15, 55, 67, 45, 12, 43, 56

Solution:

Method 1:

Step 1:

First, we find the algebraic sum of the squares for this take the square of each number and then add all of them,

The Sum of the squares = (9)² + (15)² + (55)² + (67)² + (45)² + (12)² + (43)² + (56)²

= (81) + (225) + (3025) + (4489) + (2025) + (144) + (1849) + (3136)

= 14974

Method 2:

Now we find the sum of the squares by the statistical method,

Step 1:

Determine the data set's average. (Mean)

Total numbers = 8

Total sum = 302

Statistical mean = total sum / total numbers

Statistical mean = 302 / 8

Statistical mean = 37.75

Step 2:

Determine each data point's deviation from the mean square for each of these variations.

= (9 - 37.75)²

= (15 - 37.75)²

= (55 - 37.75)²

= (67 - 37.75)²

= (45 - 37.75)²

= (12 - 37.75)²

= (43 - 37.75)²

= (56-37.75)²

Step 3:

Total the squared discrepancies(differences)

= (-28.75)² + (-22.75)² + (17.25)² + (29.25)² + (7.250)² + (-25.75)² + (5.250)² + (18.25)²

= (826.6) + (517.6) + (297.6) + (855.6) + (52.56) + (663.1) + (27.56) + (333.1)

= 3575