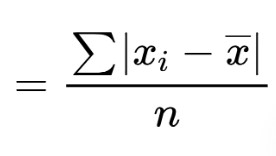Blog Worksheets Examples Practice Problems FAQs

Mean Absolute Deviation Calculator

Enter the comma separated values in the box to find mean absolute deviation using Mean Absolute Deviation Calculator

How to use the Mean Absolute Deviation Calculator?

Stick to the instructions below to use the MAD calculator.

Enter the data values.
Separate the values with commas.
Click Calculate.

Mean Absolute Deviation (MAD) Calculator

This tool is designed to find the MAD of a data set. The mean absolute deviation calculator provides the results with a well-explained step-by-step process.

What is the mean absolute deviation (MAD)?

This particular value informs you about the difference between a data set value and its mean on average. With this knowledge, one makes an assumption about how diverse a dataset is.

But it should be noted that MAD is largely affected by individual values. For example, if every data set value differs from the mean by 3 or 2 points but there are two values that differ by 20 or 30 points, the results of MAD will not be reliable.

It is because those extreme values will dramatically change the value of absolute deviation. Therefore, standard deviation and variation are used more often in statistics.

MAD formula:

The formula for Mean Absolute deviation is as follows:

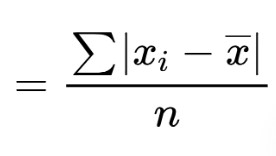
mean absolute deviation formula

In this formula:

Σ is the summation symbol. It means “add”.
x_i is each individual value.
X bar is the mean of the whole data.

n is the number of values.

How to calculate Mean absolute deviation?

First of all, find the mean of the data set. You can use the mean calculator as well. After that subtract each value from the mean value. Add the resultant values and divide with the n i.e total number of values.

Example:

What is the mean absolute deviation for the following data?

(3, 8, 10, 17, 24, 27).

Input data:

Data set = 3, 8, 10, 17, 24, 27

Total number of values (n) = 6

Formula:

Solution:

Step 1: Find mean.

X_mean = 3 + 8 + 10 + 17 + 24 + 27 / 6

= 89 / 6

= 14.833

Step 2: Subtract each value from the mean.

xi - X̄	\|xi - X̄\|
-11.833	11.833
-6.833	6.833
-4.833	4.833
2.167	2.167
9.167	9.167
12.167	12.167

Step 3: Add all the values.

= 11.833 + 6.833 + 4.833 + 2.167 + 9.167 + 12.167

= 47

Step 4: Divide by n.

= 47/ 6

= 7.833