Coefficient of variation Calculator
Use the coefficient of variance calculator to find the standard deviation value relative to the mean. Calculate the sample or population coefficient of variation depending on the data type. Each step is mentioned along with a separate table of essential values.
What is the coefficient of variation?
It is another measure of variability. It is a ratio between the standard deviation and the sample or population mean. The best use of the CV is when you want to compare measurements in different units.
See the following example. The paint prices of a certain international brand changed in two countries over the period of 6 years as follows.
USA | Pakistan |
| 30$ | 5000 PKR |
| 25$ | 4570 PKR |
| 26$ | 4900 PKR |
| 29$ | 4200 PKR |
| 32$ | 5100 PKR |
| 30$ | 5250 PKR |
The standard deviation of the above datasets is 2.658 and 386.609. The variability may seem larger for the second column. But this is not the right judgment. We will need a technique that will help us to find the dispersion of the data regardless of its unit.
In such cases coefficient of variation calculator is used because the value provided will be relative to the mean of the dataset. The CV for the above datasets is 0.093 and 0.080. This makes it clear that the second set has less dispersion.
The formula of coefficient of variation:
As mentioned before, it is a ratio between the standard deviation and mean.
CV = SD / x̄
- CV is the coefficient of variation.
- SD is the standard deviation.
- X̄ is the mean.
How to calculate the coefficient of variation?
The procedure to find the coefficient of variation is the same as finding the mean and standard deviation. At the end just divide the standard deviation by the mean.
Example:
What is the coefficient of variation for the following set?
6167, 7404, 1574, 5684, 466, 2699, 215, 1429
Solution:
Step 1: Find the mean.
X̄ = 𝚺 xi / n
= 6167 + 7404 + 1574 + 5684 + 466 + 2699 + 215 + 1429
= 25638 / 8
= 3204.75
Step 2: Find the standard deviation.
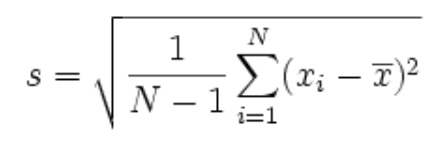
Finding the sum of squares.
= 6167−3204.75)2 + (7404−3204.75)2 + (1574−3204.75)2 + (5684−3204.75)2 + (466−3204.75)2 + (2699−3204.75)2 + (215−3204.75)2 + (1429−3204.75)2
= 55063079.5
Divide by n-1. Take the square root.
= 55063079.5 / 8-1
= 55063079.5 / 7
Take the square root.
= √ 55063079.5 / 7
= 2803.66
Step 3: Calculate the CV.
= 2803.66 / 3204.75
= 0.875
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
