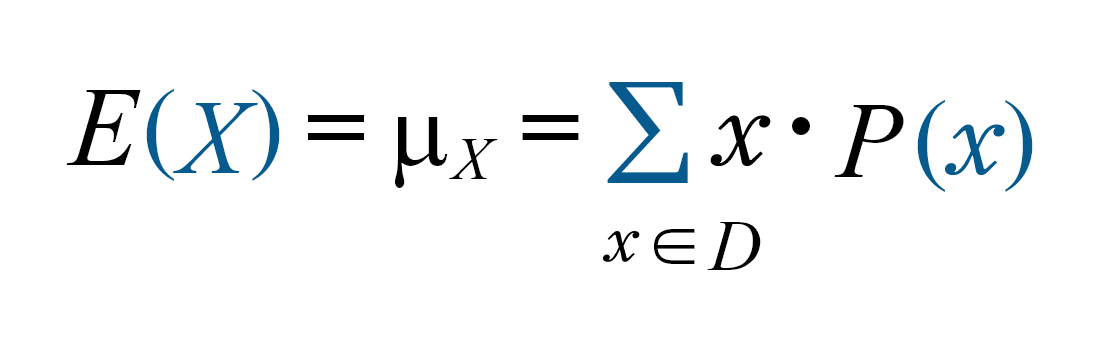Expected Value Calculator
We love feedback
How would you rate your experience?
Very Poor
Poor
Average
Good
Excellent
Any thing you want to tell us?
Feedback Submitted Successfully.
How to use the expected value calculator?
Follow the steps below to use the expected value calculator:
- Put all possible outcome values of “X” in the given box.
- Put all the probabilities of an outcome “P (x)” in the below box.
- To the expected value click on the “Calculate” button
- To more inputs click on the “Reset” button.
| x | P(x) | x × P(x) | |
|---|---|---|---|
| ∑xi = | ∑ P(xi) = | ∑xi × P(xi) = | |
We love feedback
How would you rate your experience?
Very Poor
Poor
Average
Good
Excellent
Any thing you want to tell us?
Feedback Submitted Successfully.
