Quartile Calculator
Find q1, q2, q3, and the interquartile range using the quartiles calculator. It is a statistical tool to assist in calculating the quartiles of any given dataset. Moreover, it is entirely free and can be used any number of times.
What is a Quartile?
The quartile is derived from the quarter because these are such places of a dataset that indicate the fourth part of it. It is not a number from the dataset itself but a position.
These positions are basically medians according to different ranges within the data. Fundamentally, there are 3 quartiles.
1st Quartile:
A dataset has 100 percentiles. the 1st quartile is up to the 25th percentile. It is denoted by Q1. This quartile is the median of the lower half of the data.
2nd Quartile:
The second quartile is represented by Q2 and is also known as the median of the data. It divides the set into two parts or 50/50 percentiles.
3rd Quartile:
The median of the upper half of the data set is called the 3rd quartile i.e Q3. It makes a ratio of 3:1 and is the 75th percentile of the dataset.
IQR:
IQR is the acronym for interquartile range. It leaves 25 percent from both slides and accounts for the 50 percent of data in between.
Though the median does a fair job of finding the average, we still need quartiles for sets that are more scattered and have polar values i.e extremely high or low. This technique divides data into different parts and finds many averages of the same set.
Quartile formula:
There is a special formula to find quartiles. It is
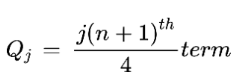
The letter “j” is the quartile number i.e 1,2, or 3. N is the total number of values.
The interquartile range is calculated by subtracting Q1 from Q3.
How to find quartiles?
Since quartiles are basically medians of different parts of the data, they can be calculated using the median formula. Alternatively, you can use the formula above.
Below you will find an example of both methods.
Example:
10,10,34,23,54,9,12,6,40
Solution:
Step 1: Find the median.
N = 1
= (n+1) / 2
= (9+1) / 2
= 10 / 2
= 5
Sort the data and find the 5th term.
= 6,9,10,10,12,23,34,40,54
= 12 is the 5th term.
It is q2.
Step 2: Divide the data at q2. Find the medians of the upper and lower half.
Lower set = 6,9,10,10
= [(n/2)th term + (n+2/2)th term]/2
= (4/2 + 4+2/2)/2
= (9 + 10)/2
= 19/2
= 9.5
It is the q1 or first quartile.
upper set = 23,34,40,54
= [(n/2)th term + (n+2/2)th term]/2
= (4/2 + 4+2/2)/2
= (34 + 40)/2
= 74/2
= 37
This is q3 or the third quartile.
Example:
10,10,34,23,54,9,12,6,40
Solution:
Step 1: Arrange the data.
= 6,9,10,10,12,23,34,40,54
Step 2: Use the formula to find the q1.
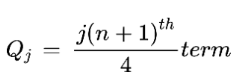
Q1 = 1(9 + 1) / 4
= 10/4
= 2.5th term
= 2nd term + 0.5(3rd term - 2nd term).
= 9 + 0.5 (10-9)
= 9 + 0.5 (1)
= 9 + 0.5
= 9.5
Q2 = 2(9+1) / 4
= 20/4
= 5th term
= 12
Q3 = 3(9+1) / 4
= 30 / 4
= 7.5th term
= 7th term + 0.5(8th term - 7th term).
= 34 + 0.5 (40-34)
= 34 + 0.5 (6)
= 34 + 3
= 37
Hence, the results are the same for all the methods, and among all these methods, using the quartiles calculator is the most time-saving.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
