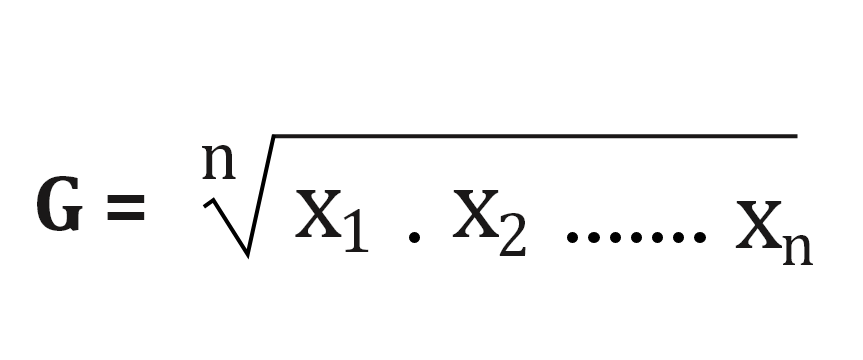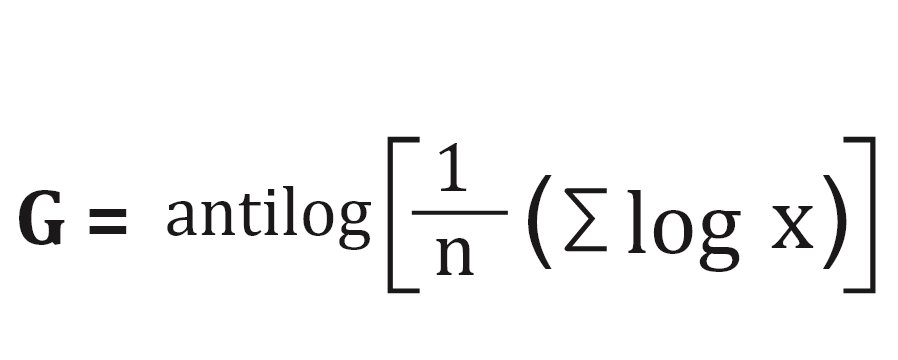Geometric Mean Calculator

What is geometric mean in statistics?

A geometric mean is a type of average, defined as the nth positive root of the product of the terms of the data set.

Formula of Geometric mean:

There are two different formulas to calculate the geometric mean of the given data:  

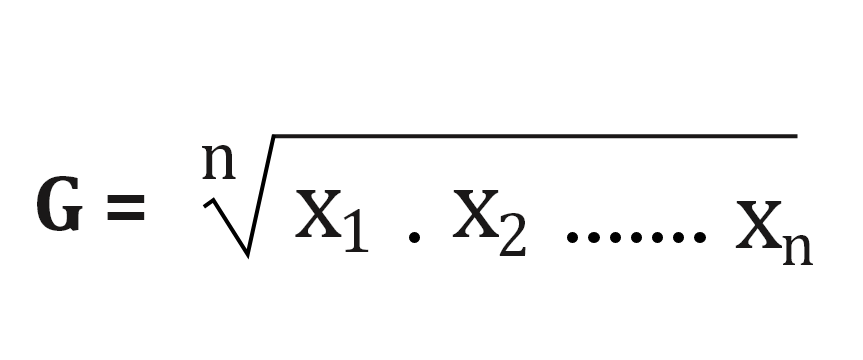
In the above formula:

• X2. X3…. Xn
• “n” is the total number of terms

When “n” is very large we use the following formula:

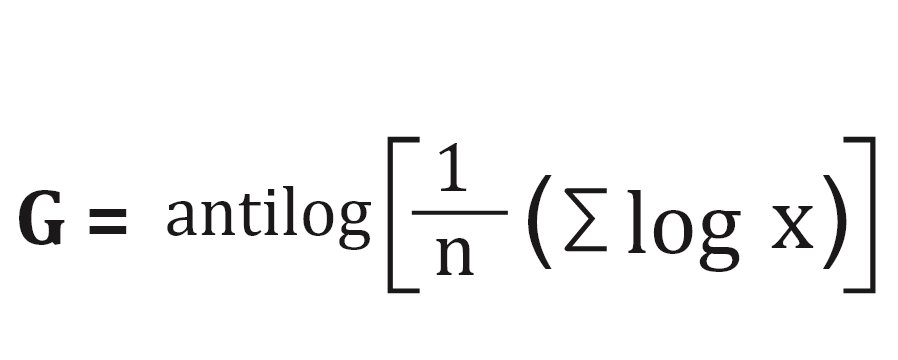
• “Σ (log X)” is the sum of the logarithm of the values.

Advantages and disadvantages of geometric mean:

In this section, we’ll discuss some pros and cons of the term geometric mean.

Advantages of Geometric Mean:

Useful for calculating average rates of change:

Geometric mean is useful in calculating the average rate of change, such as growth rate, decay rate, or interest rate, over a period of time.

Appropriate for skewed distributions:

Geometric mean is appropriate for distributions that are skewed, or where the data are clustered around small values since outliers do not influence it.

Useful for averaging ratios:

Geometric mean is useful in situations where ratios need to be averaged, such as when calculating average stock returns.

Easy to compute:

Geometric mean is easy to calculate, as it involves taking the nth root of the product of n numbers.

Disadvantages of Geometric Mean:

Sensitive to small values:

Geometric mean is sensitive to small values, meaning that small values can have a large impact on the resulting value.

Cannot be used for negative values:

Geometric mean cannot be used for data with negative values, as it requires the calculation of a logarithm of the data.

Not appropriate for sums:

Geometric mean is not appropriate for sums, as it does not take into account the magnitudes of the individual values.

Can be misleading in some situations:

Geometric mean can be misleading in situations where some values are much larger or smaller than others.

Examples:

In this section, we’ll discuss the steps for calculating the geometric mean of ungrouped data.

Example 1:

10, 12, 18, 20, 25, 30, 35

Solution:

Step 1: Extract the data.

X = 10, 12, 18, 20, 25, 30, 35

n = 7

Step 2: Put the values in the formula.

Geometric mean = (X₁ * X₂ . . .* X_n)^1/n

Geometric mean = (10 * 12 * 18 * 20 * 25 * 30 * 35)^1/7

Geometric mean = (1134000000) ^0.1429             

Geometric mean = 19.6570