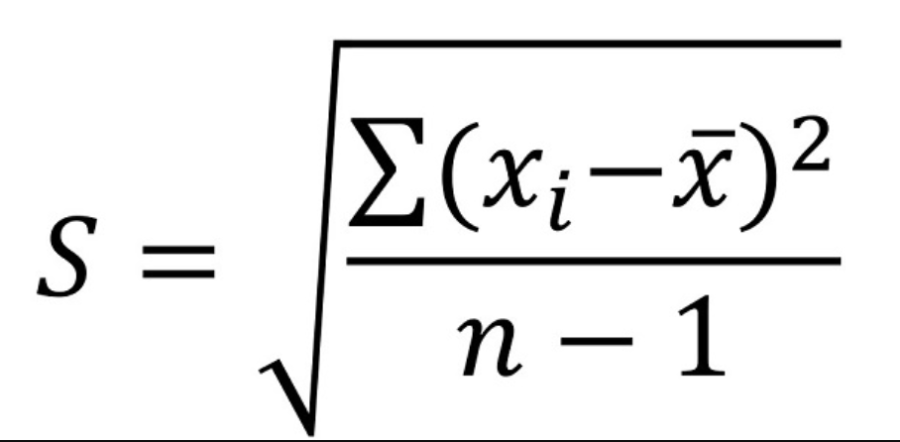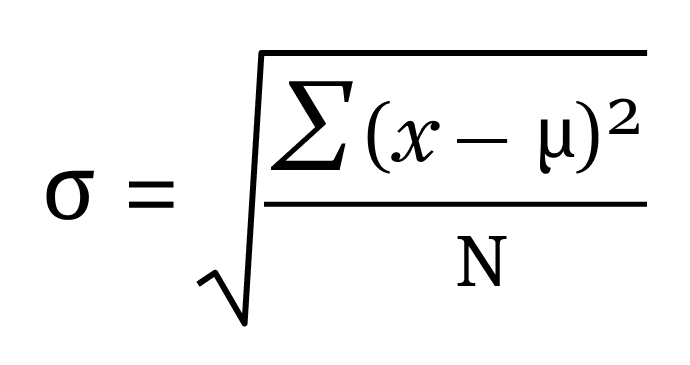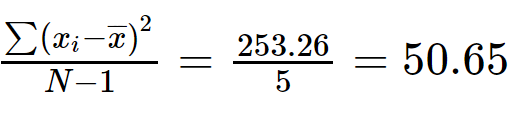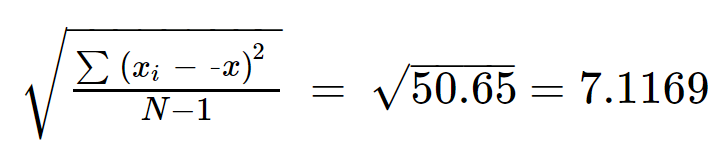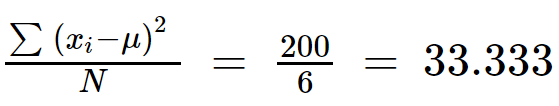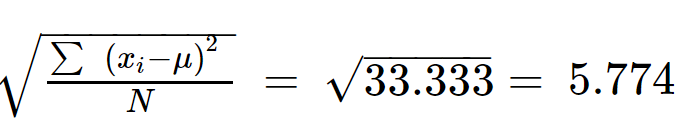Let’s explore a few key points such as standard deviation definition, how to find standard deviation without using a relative standard deviation calculator, and the standard deviation equation.
What is the standard deviation?
A measure of the extent to which numbers are spread out.
Standard Deviation is a statistic that measures the dispersion of a dataset relative to its mean and is calculated as the square root of the variance. It is denoted by the Greek symbol sigma σ.
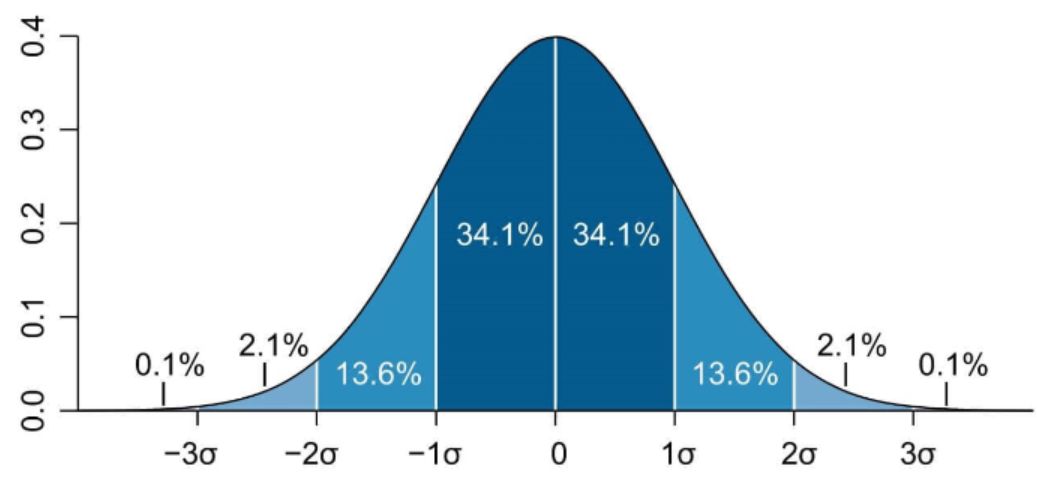
Below, you can find the plot of a normal distribution with a width of 1 band.
Standard Deviation Formula
The standard deviation formula can be expressed by taking the square root of the variance.
Sample Standard Deviation Formula
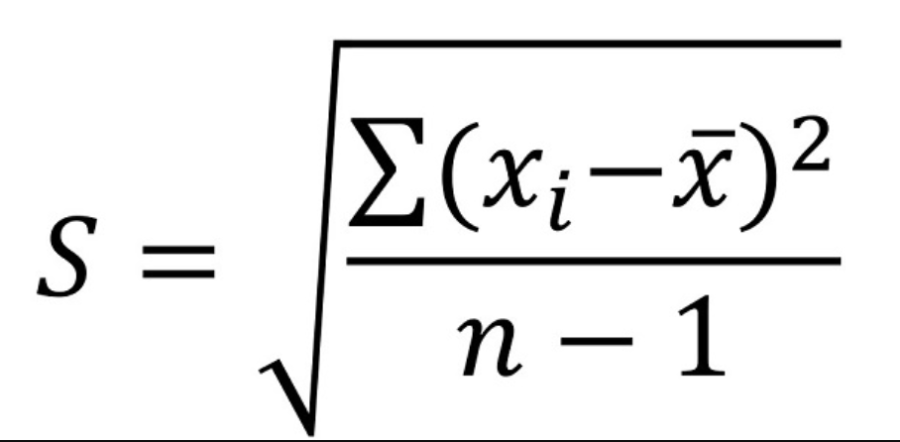
- s refers to sample standard deviation
- N is the number of observations
- xi is the observed values of the sample item, and
- x̄ is the mean value of the sample
Population Standard Deviation Formula
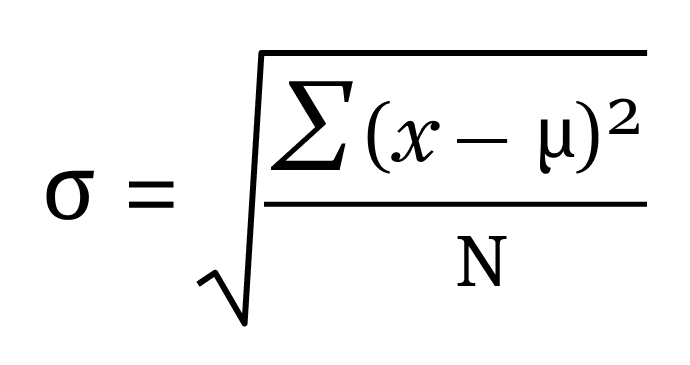
- σ refers to population standard deviation
- N is the size of the population
- xi is the observed values from the population, and
- μ is the population mean
How To Calculate Standard Deviation?
Standard deviation calculation can be carried out using the mean and standard deviation calculator above. However, we will explain the method to calculate SD with examples.
Example 1: Calculate Sample Standard Deviation
Find the standard deviation of the given sample:
30, 20, 28, 24, 11, 17
Solution
Step 1: Calculate the mean value of sample data:
N = 6
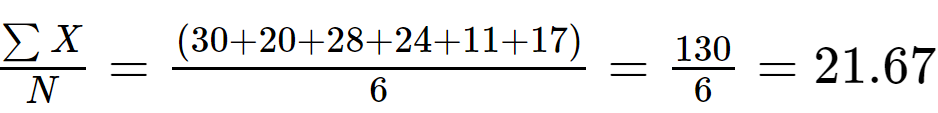
Step 2: Calculate (xi - x̄) by subtracting the mean value from each value of the data set and calculate the square of differences to make them positive.
| Data Values (xi) | xi - x̅ | (xi - x̅ )2 |
| 30 | 30 - 21.67 = 8.33 | (8.332)2 = 69.4 |
| 20 | 20 - 21.67 = -1.67 | (-1.672)2 = 2.78 |
| 28 | 28 - 21.67 = 6.33 | (6.332)2 = 40 |
| 24 | 24 - 21.67 = 2.33 | (2.332)2 = 5.43 |
| 11 | 11 - 21.67 = -10.67 | (-10.672)2 = 113.85 |
| 17 | 17 - 21.67 = -4.67 | (-4.672)2 = 21.80 |
Step 3: Get the sum of all values for (xi - x̅)2.
∑(xi - x̅)2 = 69.4 + 2.78 + 40 + 5.43 + 113.85 + 21.80
∑(xi - x̅)2 = 253.26
Step 4: Divide ∑(xi - x̅)2 with (N-1).
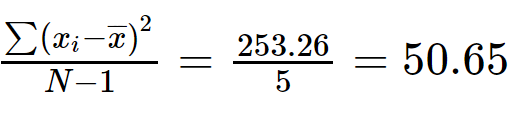
Variance = 50.65
Step 5: Take the square root of ∑(xi - x̅)2/(N-1) to get the standard deviation.
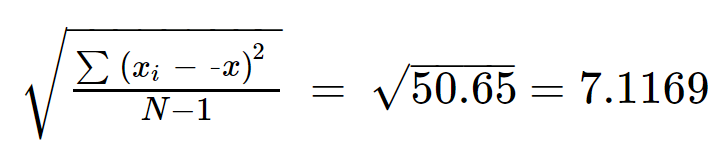
s = 7.1169
The above sample standard deviation calculator can be used to check the result of this example.
Example 2: Calculate Population Standard Deviation
Calculate standard deviation of the given population data:
10, 12, 18, 14, 21, 27
Solution
Step 1: Calculate the expected value of population data:
N = 6
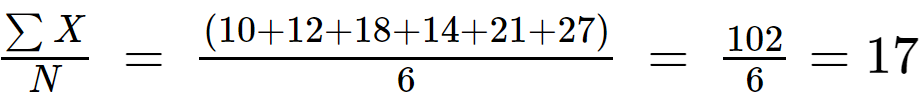
Step 2: Calculate (xi - µ) by subtracting the mean value from each value of the data set and calculate the square of differences to make them positive.
| Data Values (xi) | xi - µ | (xi - µ)2 |
| 10 | 10 - 17 = -7 | (-7)2 = 49 |
| 12 | 12 - 17 = -5 | (-5)2 = 25 |
| 18 | 18 - 17 = 1 | (1)2 = 1 |
| 14 | 14 - 17 = -3 | (-3)2 = 9 |
| 21 | 21 - 17 = 4 | (4)2 = 16 |
| 27 | 27 - 17 = 10 | (10)2 = 100 |
Step 3: Get the sum of all values for (xi - µ)2.
∑(xi - µ)2 = 49 + 25 + 1 + 9 + 16 + 100
∑(xi - µ)2 = 200
Step 4: Divide ∑(xi - µ)2 with (N).
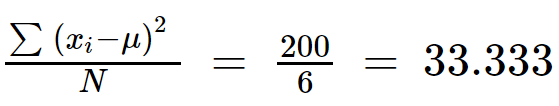
Variance = 33.333
Step 5: Take the square root of ∑(xi - µ)2/N to get the standard deviation.
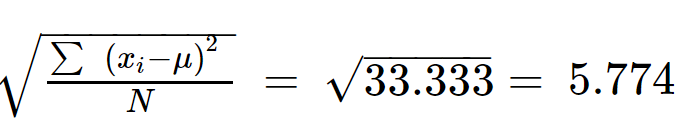
σ = 5.774
Use the population standard deviation calculator above to cross-check the values for SD calculations.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
