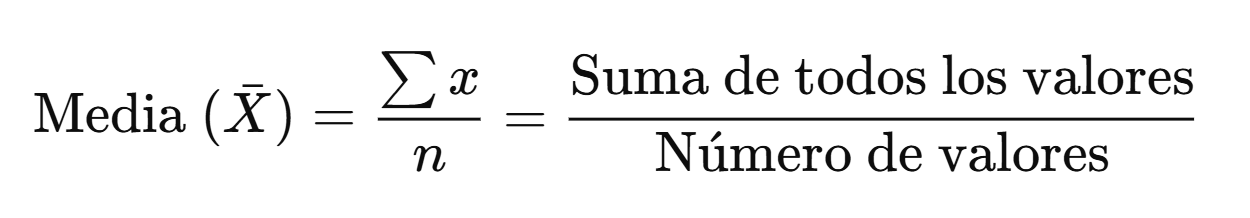Calculadora de Media
Encuentre la media de un conjunto de datos discretos y conozca las diferentes propiedades de los datos usando esta calculadora.
Por ejemplo, la calculadora de medias, además de proporcionar la media con una solución paso a paso, proporciona el número total de datos, la matriz ordenada y los valores de los datos más pequeños y más grandes.
¿Cuál es la media del conjunto de datos?
Una palabra para describir la media es «valor promedio». Un valor que se encuentra entre ambos extremos de los datos.
Existen otros tipos de medias como la armónica y la geométrica pero la base de todas ellas o la “Media Actual” es la media aritmética.
Fórmula Media
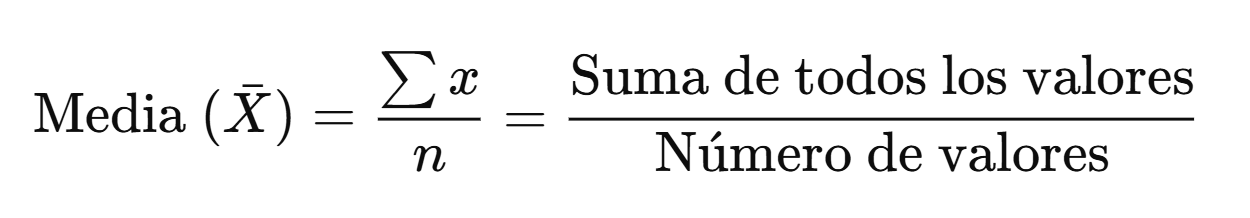
La barra X pequeña es la notación utilizada para la media en matemáticas, aunque se representa de forma diferente en estadística. N es el número de valores del conjunto de datos. La notación sigma significa suma.
Cómo calcular la media?
Encuentra la suma de todos los datos. Cuenta cuántos valores hay en los datos. Divide la suma entre ese número. El resultado es la media de los datos.
Ejemplo de cálculo de la media para datos no agrupados:
Encuentra la media del siguiente conjunto de datos:
10, 10, 34, 23, 54, 9, 10, 2, 38, 23, 38, 23, 21
Solución:
Siga estos pasos para calcular la media de datos no agrupados
Paso 1: Agrega los datos.
= 2+9+10+10+10+21+23+23+23+34+38+38+54
= 295
Paso 2: Cuente los valores.
Hay un total de 13 valores.
Paso 3: Divide la suma por 13.
= 295/13
= 22.692
La media de los datos no agrupados es 22,692.
Ejemplo de cálculo de la media para datos agrupados:
Considere el siguiente conjunto de datos que representa las calificaciones obtenidas por los estudiantes en un examen. Las calificaciones se agrupan en intervalos:
Marcas (Intervalo) | Frecuencia (f) |
0 - 10 | 3 |
10 - 20 | 5 |
20 - 30 | 8 |
30 - 40 | 4 |
40 - 50 | 2 |
Calcular la media de los datos dados.
Solución
Siga estos pasos para calcular la media de datos agrupados
Paso 1: Calcular los puntos medios
Marcas (Intervalo) | Frecuencia (f) | Punto medio (x) | f⋅x |
0 - 10 | 3 | 5 | 15 |
10 - 20 | 5 | 15 | 75 |
20 - 30 | 8 | 25 | 200 |
30 - 40 | 4 | 35 | 140 |
40 - 50 | 2 | 45 | 90 |
Paso 2: Calcular la suma de f⋅x
Σ(f⋅x) =15+75+200+140+90=520
Paso 3: Calcular la frecuencia total
Σf = 3+5+8+4+2=22
Paso 4: Calcular la media
Media=Σ(f⋅x)/ Σf
=520 / 22
≈23.64
La media de los datos agrupados es 23,64.
Preguntas Frecuentes
¿Cómo encontrar la media?
La media de cualquier tipo de conjunto de datos, ya sea que se trate de un conjunto de datos de muestra/población y de un conjunto de datos de números positivos o negativos, encuentre su valor usando la fórmula de la media siguiendo los dos simples pasos a continuación.
En primer lugar, encuentre la suma de los valores sumándolos todos.
Utilizando su fórmula, divida la suma por el número de elementos del conjunto de datos dado.
¿Cómo sacar el media con números positivos y negativos?
The mean of the negative numbers is found similar to the finding of the mean of the positive data set by adding or subtracting the data values according to the given sign and dividing by the number of elements of any data set.
¿Qué relación existe entre la media, la mediana y la moda?
La relación entre la media, la mediana y la moda se puede expresar mediante la ecuación de relación empírica de Karl Pearson, que muestra la distribución sesgada y se enuncia como:
3 × Mediana = Moda + 2 × Media
¿Cuál es la media de los primeros 5 números compuestos?
La media de los primeros cinco números compuestos utilizando la fórmula de la media es igual a “7,4” y los primeros cinco números compuestos son 4, 6, 8, 9 y 10. Para verificar este valor, utilice nuestra calculadora de media anterior que proporciona la respuesta a cualquier número de conjuntos de datos.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Feedback Submitted Successfully.
