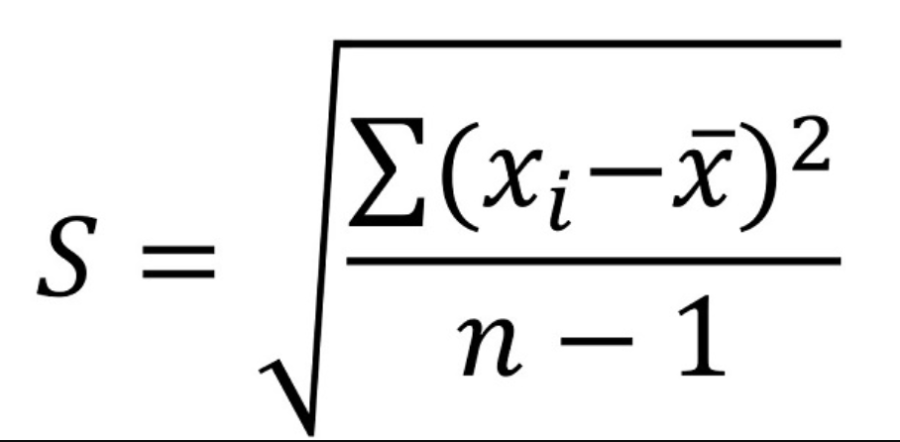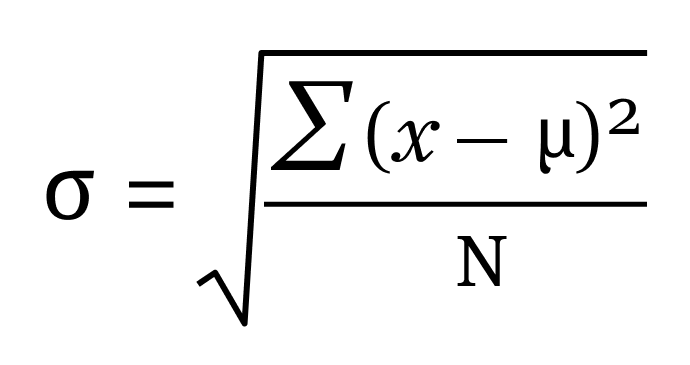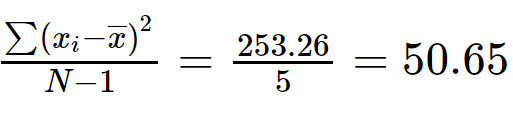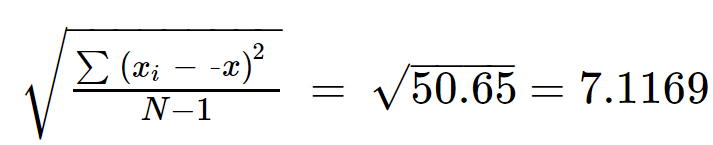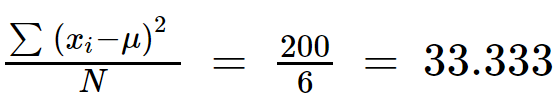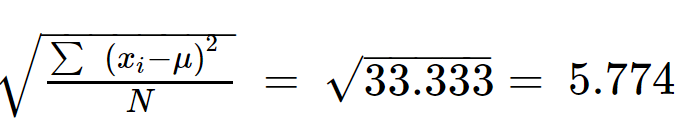Vamos explorar alguns pontos-chave, como a definição do desvio padrão, como encontrar o desvio padrão sem usar uma calculadora de desvio padrão relativo e a equação do desvio padrão.
Qual é o desvio padrão?
Uma medida da extensão em que os números estão espalhados.
O Desvio Padrão é uma estatística que mede a dispersão de um conjunto de dados em relação à sua média e é calculado como a raiz quadrada da variância. É denotado pelo símbolo grego sigma σ.
Abaixo, você encontra o gráfico de uma distribuição normal com largura de 1 faixa.
Fórmula de Desvio Padrão
A fórmula do desvio padrão pode ser expressa calculando a raiz quadrada da variância.
Exemplo de fórmula de desvio padrão
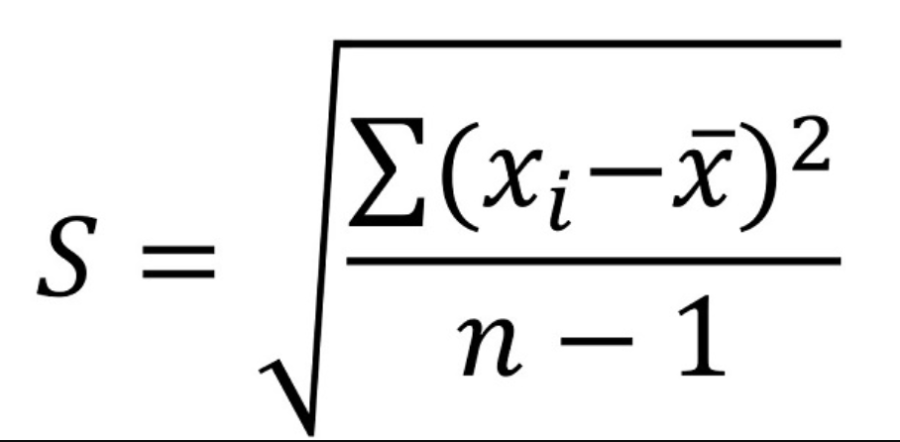
- é refere-se ao desvio padrão da amostra
- N é o número de observações
- x eu são os valores observados do item da amostra, e
- x̄ é o valor médio da amostra
Fórmula de desvio padrão populacional
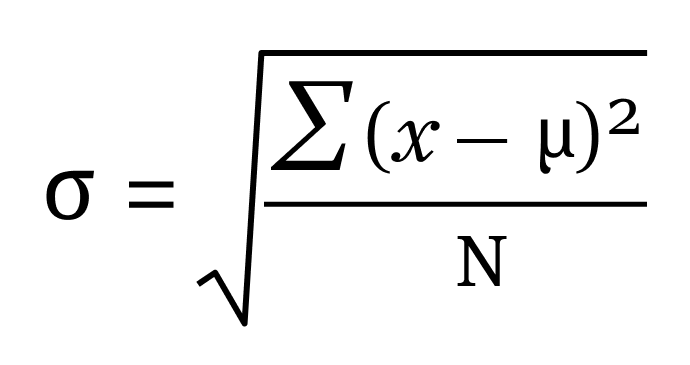
- σ refere-se ao desvio padrão da população
- N é o tamanho da população
- x eu são os valores observados da população, e
- μ é a média da população
Como calcular o desvio padrão?
Cálculo do desvio padrão pode ser realizado usando a calculadora de média e desvio padrão acima. No entanto, explicaremos o método de cálculo do SD com exemplos.
Exemplo 1: Para Desvio Padrão Amostral
Encontre o desvio padrão da amostra dada:
30, 20, 28, 24, 11, 17
Solução
Passo 1: Calcule o significar valor dos dados de amostra:
N = 6
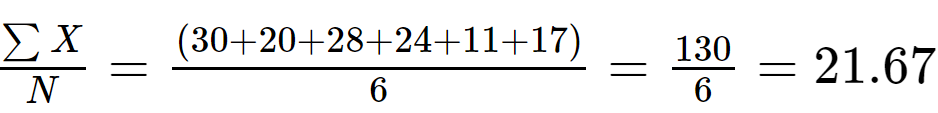
Passo 2: Calcular (x eu - x̄) subtraindo o valor médio de cada valor do conjunto de dados e calculando o quadrado das diferenças para torná-las positivas.
| Valores de dados (x eu ) | x eu - x̅ | (x eu -x̅) 2 |
| 30 | 30 - 21,67 = 8,33 | (8.332) 2 = 69,4 |
| 20 | 20 - 21,67 = -1,67 | (-1.672) 2 = 2,78 |
| 28 | 28 - 21,67 = 6,33 | (6.332) 2 = 40 |
| 24 | 24 - 21,67 = 2,33 | (2.332) 2 = 5.43 |
| 11 | 11 - 21,67 = -10,67 | (-10.672) 2 = 113,85 |
| 17 | 17 - 21,67 = -4,67 | (-4.672) 2 = 21,80 |
Etapa 3: Obtenha a soma de todos os valores para (x eu -x̅) 2 .
∑(x eu -x̅) 2 = 69,4 + 2,78 + 40 + 5,43 + 113,85 + 21,80
∑(x eu -x̅) 2 = 253,26
Passo 4: Divida ∑ (x eu -x̅) 2 com (N-1).
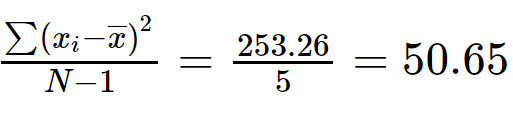
Variância = 50,65
Etapa 5: Tire a raiz quadrada de ∑(x eu -x̅) 2 /(N-1) para obter o desvio padrão.
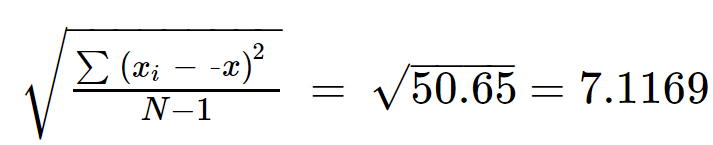
s = 7,1169
A calculadora de desvio padrão de amostra acima pode ser usada para verificar o resultado deste exemplo.
Exemplo 2: Para População Desvio padrão
Encontre o desvio padrão dos dados populacionais fornecidos:
10, 12, 18, 14, 21, 27
Solução
Passo 1: Calcule o valor esperado dos dados populacionais:
N = 6
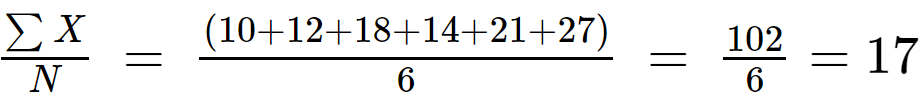
Passo 2: Calcular (x eu - µ) subtraindo o valor médio de cada valor do conjunto de dados e calculando o quadrado das diferenças para torná-las positivas.
| Valores de dados (x eu ) | x eu - µ | (x eu - µ) 2 |
| 10 | 10 - 17 = -7 | (-7) 2 = 49 |
| 12 | 12 - 17 = -5 | (-5) 2 = 25 |
| 18 | 18 - 17 = 1 | (1) 2 = 1 |
| 14 | 14 - 17 = -3 | (-3) 2 = 9 |
| 21 | 21 - 17 = 4 | (4) 2 = 16 |
| 27 | 27 - 17 = 10 | (10) 2 = 100 |
Etapa 3: Obtenha a soma de todos os valores para (x eu - µ) 2 Então então
∑(x eu - µ) 2 = 49 + 25 + 1 + 9 + 16 + 100
∑(x eu - µ) 2 = 200
Passo 4: Divida ∑(x eu - µ) 2 com (N).
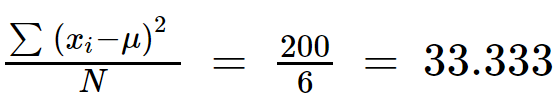
Variância = 33,333
Etapa 5: Tire a raiz quadrada de ∑(x eu - µ) 2 /N para obter o desvio padrão.
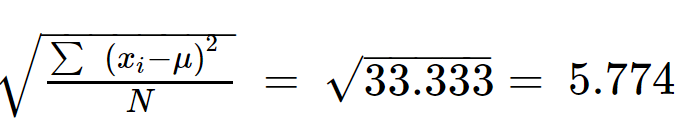
σ = 5,774
Use a calculadora de desvio padrão populacional acima para verificar os valores dos cálculos de SD.
Very Poor
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Download
